High-temperature faulting, Heart Mountain Detachment, Wyoming
Abstract
The Heart Mountain Detachment is a nearly horizontal (2° slope) fault that underlies a 3400-square kilometer by 1.5-kilometer thick block of rock; this block slid up to 45 km on this fault about 50 million years ago. Understanding how this unusual fault worked can help in unravelling the mechanisms involved in earthquakes and landslides, which claim many lives and damage much property every year. The Heart Mountain Detachment is remarkably thin for the amount of movement it has experienced, being only millimeters wide in many places, and the rocks beneath the fault are commonly undeformed. The mechanisms of movement of this fault are elucidated by a detailed study of samples of fault rocks. The fault contains finely-crushed cataclasite; in some places, it also contains ‘armored grains’ that display a coating of very fine-grained carbonate minerals that are thought to have formed from high-temperature (>800 C) decomposition of carbonate minerals due to frictional heating accompanying early stages of fault movement. There is little evidence for multiple episodes of movement on the fault, as would be indicated by cross-cutting cataclasite zones, brecciated breccias, and the like: it is likely that most if not all movement of the block above the fault happened as a single event. This study shows that the cataclasites contain extremely-fine grained (tens of nanometers or less) fragments, which likely reduced the fault’s coefficient of friction enough to allow the block above it to move easily. These rocks contain unusual Mg-silicate minerals that likely formed during fault movement. Contradicting the assertions of some workers, geochemical data from this study shows that the fault has not been the site of any significant amount of pressure solution. Physical modeling of block movement down a gentle slope shows that the fault must have had a very low coefficient of friction, consistent with the fault’s thinness as well as with evidence that fluids, which can also lubricate faults when at high pressure, commonly escaped from the fault zone and thus did not build up significant pressures. Modeling shows that the maximum speed of the block above the fault, given that the movement occurred in a single catastrophic episode, was on the order of tens of miles per hour, and that the entire movement took on the order of minutes.
Introduction
Accurate prediction of earthquakes and landslides can potentially save thousands of lives per year worldwide. For it to be successful, such forecasting must be based squarely on a robust understanding of the mechanics of rock failure, based on theory as well as laboratory and field-based observations. The Heart Mountain Detachment Fault in northwestern Wyoming provides an outstanding natural laboratory for studying an enormous block slide and better constraining processes involved in near-surface rock failure. About 50 million years ago, this nearly-horizontal (estimated 2° slope at the time of movement) fault accommodated the downslope movement of a 3400 km2 by 1–to 2-km thick block of carbonate and andesitic volcanic rock up to 45 kilometers, likely in a matter of minutes (e.g., Beutner and Gerbi, 2005; Craddock et al., 2009). This remarkable movement is thought to have been facilitated by a process known as calcining, whereby frictional heating on the fault caused carbonate rock to dissociate into CaO + CO2 (Han et al., 2007); CO2 presumably acted to raise the fluid pressure and decrease effective stress in the fault zone and thus allow easier movement. CO2 also recombined with calcium compounds (CaO and Ca(OH)2) to form nanometer-sized particles in a process known as sintering (Anders et al., 2010; Han et al., 2007). These particles may have further facilitated movement, particularly if their shape combined with small size altered the fault’s coefficient of friction (Han et al., 2007).
Despite the importance of the calcining and sintering mechanisms in failure of carbonate-bearing rocks, which are common worldwide, there is little published verification of it. Rowe et al., (2012) describe this process in association with earthquake occurrence on a thrust fault in Naimibia, and Rempe et al., (2014) noted textures consistent with calcining in the Tremonti Fault, Italy. Anders et al. (2010) documented large aggregated “armored grains” in the Heart Mountain Detachment, with Bouillier et al. (2009) describing clay-rich armors surrounding some cataclasite grains in a Taiwanese thrust fault. Armored grains are described later in this report; no detailed studies exist of the textures of these rocks, particularly the size and shape of the individual grains that controlled the mechanical properties of the detachment while it was active. This study focuses on sampling of the Heart Mountain Detachment Fault at several localities and evaluating the petrography of fault rocks using standard thin section microscopy as well as Scanning Electron Microscopy (SEM), augmented by whole-rock geochemistry, to evaluate processes that operated within the fault zone while it was active.
Geology
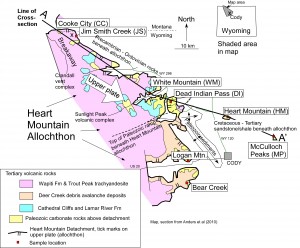
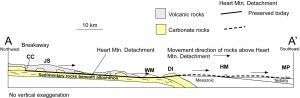
To evaluate the mechanics of movement on the Heart Mountain Detachment, its geologic context must be adequately characterized. This fault is shown in Figure 1; a northwest-southeast cross-section is shown in Figure 2.
Figure 1. Geologic map of Heart Mountain Detachment Fault (bold black line separating colored upper plate from white lower plate in figure) and adjacent rocks, northwestern Wyoming. White arrow labeled “Upper plate” shows direction of movement of rocks above the Detachment (the colored units west of the detachment on the map). Sample locations discussed in text are shown. Geology is modified from Anders et al. (2010).
Figure 2. Geologic cross-section of Heart Mountain Detachment along line A-A’ (see Figure 1 for location). Fault lies atop Paleozoic carbonate rocks northwest of Dead Indian Pass, where it cuts across them (“ramp” shown on Figure 1). Southeast of Dead Indian, the detachment places Paleozoic carbonate rocks atop younger Mesozoic and Tertiary shales and sandstones of the Bighorn Basin. Carbonate rocks at McCulloch Peaks (MP on section) must have traveled at least 42 km in the direction of this section, which is roughly parallel to movement direction based on kinematic indicators in and above the fault zone.
As shown in Figure 2, the Heart Mountain Detachment has broken parallel or nearly parallel to sedimentary bedding along nearly its entire length (also see Figure 3), except for a portion at Dead Indian Pass (DI on the cross-section), where it cuts up and across bedding. Regional reconstructions indicate that the fault dipped about 2° to the southeast at the time it moved. Andesitic volcanic rocks above the fault were deposited about 50 million years ago in association with two major volcanic centers, the Sunlight Peak and the Crandall volcanic complexes (Figure 1); numerous dikes accompany these extrusive rocks. The faulting is nearly synchronous with volcanism, leading several investigators starting with Pierce (1973) to propose that volcano-related doming provided a gentle subsurface slope down which a large block of rock could slide (Beutner and Hauge, 2009), a subterranean hot spring system that could have weakened rock (Douglas et al., 2003; Templeton et al., 2005), and a source of tremors that could have triggered the massive slide. It seems likely that the thick block of carbonate rocks, overlain by volcanic rocks, started to move in a relatively small area, and that processes triggered by that movement led to a much-larger catastrophic failure that led to a single block the size of Rhode Island breaking loose at its northwest end (“breakaway” on Figures 1 and 2), accelerating downslope, pulling apart as it did so (see separated blocks above detachment north of Dead Indian Pass in Figure 2), then breaking out onto the existing land surface and sliding tens of kilometers. Heart Mountain (HM), one of these blocks, stands prominently over the town of Cody, Wyoming.
The formerly-continuous carbonate rock above the Heart Mountain Detachment north of Dead Indian Pass has been extended by about 100%, with the gaps between carbonate blocks being filled with volcanic rocks. There is remarkably little internal deformation in the carbonate blocks above the detachment – bedding can be traced continuously and horizontally the length of the block in many instances. A southeasterly direction of movement of rocks above the fault is deduced on the basis of movement-direction (kinematic) indicators (grooves of various forms in this case) in the fault at several localities (e.g., Malone et al., 1999), as well as on the distribution of fault blocks such as Heart Mountain and McCulloch Peaks southeast of their only geologically-sensible source. There has been a bit of controversy about the relationship between the volcanic rocks and the faulting, with Pierce (1973) stating that the carbonate rocks simply gave way and slid downslope, spreading apart as they did so and leaving large bare patches of fault surface exposed to the elements. However, before erosion could act on this surface, Pierce proposed that the fault was almost immediately buried by volcanic rocks, which were erupted at least in part due to the pressure release brought about by the sliding away of so much carbonate rock. One might expect that if this were the case, the volcanic rocks would be largely flat-lying, burying the carbonate blocks. This model, however, has fallen into disfavor (Hague, 1993), as volcanic rocks that overlie the fault were not deposited onto a pre-existing surface but instead are in fault contact with underlying carbonates. Observations at Jim Smith Creek (Figure 3) show numerous listric faults in the volcanic rocks flattening and ending at the detachment, indicating that the volcanic rocks were in fact faulted down onto the detachment during movement on it. Geologic mapping also shows that the volcanic rocks are tilted in many places, consistent with movement on listric normal faults soling onto the detachment (Hauge, 1993).
Above the detachment, the volcanic rocks are crosscut by a peculiar structure that is commonly associated with the detachment: clastic dikes. These features (Figure 4) contain fine-grained fragments of rock, mainly carbonate, broken by faulting and mixed with fluid (water and/or CO2); this fluid was injected upward from the fault as it was moving (e.g., Craddock et al., 2012). The clastic dikes show the typical zig-zag pattern that was controlled by local stress orientations during dike propagation. Clastic dikes are best-developed at White Mountain, where they extend over a hundred meters into the upper plate above the detachment and are in places over a meter wide; they also are noted at Heart Mountain and Dead Indian Pass.
Figure 3. Heart Mountain Detachment Fault at Jim Smith Creek, Wyoming. Carbonate rocks below the fault are Ordovician Bighorn Dolomite; bedding is readily visible. These rocks are locally brecciated at and near the fault but deformation in them is spotty. The ~50-million year old (Eocene) andesitic volcanic breccias above the detachment are little-deformed except for scattered faults that end at the detachment. The Detachment itself is a gouge zone, approximately 5 mm wide, at the contact. The fault is remarkably thin given that it has accommodated about 10 kilometers of displacement at this location.
Figure 4. Clastic dike crosscutting andesitic volcanic breccia, about 5 meters above the Heart Mountain Detachment Fault at Jim Smith Creek. The clastic dike contains broken carbonate rock fragments that were injected upward from the detachment in fluidized form during fault movement. The andesite must have been already faulted onto the detachment when the dike was emplaced, during fault movement.
As seen in the field and verified in petrographic thin section (Figure 5), the detachment is remarkably thin given its substantial amount of movement; it is furthermore remarkable for the lack of breakage (brecciation, cataclasis) in rocks immediately adjacent to it. The distinctive style of deformation at Jim Smith Creek – an extremely thin gouge zone with little to no deformation of adjacent rock – is the norm with the Heart Mountain Detachment, and is observed not only at Jim Smith Creek but at Logan Mountain, Heart Mountain, and McCulloch Peaks. Only at White Mountain is the detachment relatively thick, and there it is only 1 meter or so across.
Figure 5. Heart Mountain Detachment (“fault gouge zone” in photo) at Jim Smith Creek.
One of the many controversies surrounding the Heart Mountain Detachment involves the nature of its movement: did it move all at once (catastrophically) or did it move incrementally, in stops and starts (discontinuously)? Support exists for both models; however, one of the main bones of contention centers on whether there is evidence for only one episode of movement in terms of cross-cutting fault zones within the detachment, cross-cutting clastic dikes that formed at different times (hence implying separate faulting episodes), or fault breccias, which formed during one movement episode and then were broken into fragments that are incorporated into later-formed fault breccias. Anders (pers. comm 2015) notes that in hundreds of samples, he has never seen evidence of brecciated breccias nor, in many days in the field, has he seen cross-cutting clastic dikes; hence he concludes (also see Anders et al., 2010) that there has been one and only one episode of movement. However, Swanson (2014) and this study (Figure 6, 7) document cross-cutting clastic dikes and brecciated breccia, indicating the possibility of more than one (but likely only two) episode of movement. The cross-cutting relations indicate only that the older material was consolidated enough to behave brittly in response to applied stresses. This consolidation could have happened quickly in the case of the cataclasite: breakage of rock followed by mechanical compaction within the moving fault zone may have produced a semi-consolidated cataclasite that was nonetheless strong enough to break into fragments rather than flow as a fluidized solid. It is possible that the age differences, while real, may be small enough that both episodes of cataclasis, and both episodes of clastic dike formation, could have happened during a single protracted sliding event lasting minutes to hours. It is noteworthy that evidence of multiple episodes of movement is uncommon and that, when observed, only indicates a second episode. If the faulting did in fact take place by numerous distinct slip events, it seems likely that there would be widespread evidence of numerous episodes of movement. Thus it is reasonable to conclude that in spite of localized evidence of a second movement event, the overall nature of the faulting was catastrophic. Duration of sliding is addressed later in this report.
Figure 6. Clastic dike about 6 meters above Heart Mtn Detachment, Jim Smith Creek. Dike crosscuts andesitic volcanic breccia, and contains dark-colored andesitic cataclasite that is crosscut by lighter-colored carbonate-rich cataclasite.
Figure 7. Thin section (cross nicols) of clastic dike rock from feature shown in Figure 6. Carbonate rich cataclasite (light-colored material) incorporates a clast of andesitic cataclasite (dark); textural relations indicate the volcanic cataclasite is older than the carbonate-rich cataclasite. The age gap is unknown; only enough time is required to consolidate or cement the volcanic cataclasite into a sufficiently strong and rigid rock that it could be broken into angular fragments. This age gap could be minutes (in the case of some sort of fault-related mechanical compaction) to many years.
A notable feature of portions of the Heart Mountain Detachment, particularly at White Mountain (WM) is the abundance of “armored grains,” which comprise as much as 15-20% of some cataclasites. However, they are absent from many other locations in the Heart Mountain Detachment. Where found, these features are quasi-spherical to ovoid grains to over 1 mm in diameter, and comprise several different subtypes. 1) Some armored grains contain a core consisting of an angular rock fragment (generally carbonate but in some cases andesite), surrounded by a rim of very-fine grained material, again usually carbonate (Figure 8a). 2) Other grains are extremely fine-grained throughout; in one case (at least) the grain contains numerous spherical ‘subgrains’ (Figure 8b). 3) Still other grains contain a core of cataclasite consisting of grains having a wide range of sizes, again rimmed by extremely fine-grained carbonate (Figure 8c). 4) In rare cases, clusters of armored grains are encapsulated by a rim of fine-grained carbonate.
Figure 8a. Armored grain, White Mountain, Type 1 (clast core, armored rim). Yellow box area is shown in Figure 10.
Figure 8b (left): Armored grain type 2, White Mountain – very fine-grained material, incorporating subgrains highlighted by cathodoluminesence (right)
Figure 8c. Armored grain type 3, White Mountain – cataclasite core comprising a variety of grainsizes, with fine-grained rim.
To say that these features are enigmatic is an understatement. They are generally considered a ‘smoking gun’ for calcining and sintering: carbonate decomposed at about 800° C, and the newly-formed sintered grains aggregated, perhaps by electrostatic forces, onto nuclei as faulting waned. Mitchell et al (2015) attempted to reproduce these grains in the laboratory by heating a dolomite sample to nearly 1000° C. They observed that dolomite grains after heating showed a “rind” of very small voids (vesicles) that formed during decarbonation. They proposed that these very small vesicles could then become filled with calcite, leading to a texture that resembles an armored grain. However, this model doesn’t explain the actual textures in the cataclasites, including armoring that includes several smaller armored grains. In a unique departure, Swanson (2015) proposed that the armored grains formed by pressure solution, whereby fluids in the fault dissolved carbonate in a spherical manner, resulting in the accumulation of rims that appear to be made of insoluble residue as is typically the case with stylolites. However, petrographic and SEM analysis indicate that the rim grains are carbonate and that dissolution textures (e.g., stylolites) are rare to absent; geochemical data (presented later) also argue against significant pressure solution in these rocks.
It is noteworthy that no broken armored grains are found: it appears that their formation is the last event in the movement history of the detachment where they are observed. Their lateness with respect to faulting, combined with their restriction to a small portion of the detachment at White Mountain, implies that, although they may be instructive regarding fault processes (more on this later), their formation is not intrinsic to the mechanical behavior of the Heart Mountain Detachment.
SEM investigations
To examine the properties of fault rocks and assess the calcining – sintering hypothesis, SEM imaging and associated X-ray elemental mapping were conducted using the MSU Biology Department’s instrument. Samples were gold-coated and examined in backscattered electron imaging mode. Although the resolution became degraded at very high magnifications, imaging of fault gouge derived from volcanic rocks at Jim Smith Creek and of armored grain microspherules from White Mountain identified abundant grains having diameters significantly less than 100 nanometers (Figure 9a, 9b respectively). Preservation of such small grains during fluid infiltration and attendant tendency for recrystallization over the 50-million year time interval since faulting is unexpected: further investigations are planned to further document extremely small grains within the fault. At the same time, the existence of very fine-grained volcanic clasts in fault gouge (Figure 9a, 9b) does not directly address the calcining hypothesis, as that process affects only carbonate minerals. It does highlight the complexity of the fault mechanism problem, however, in that it opens the question of how the fault moves when carbonate is not on both sides of it – does calcining take place when volcanic rocks move over carbonates? This is not addressed in the literature.
Figure 9a (left). SEM image of fault gouge derived from andesite, Jim Smith Creek (sample 13JS5). Small, light gray grains are on the order of 100 nm in size; likely comprise pyrite or Ti-oxide. Figure 9b (Right). SEM image of microspherule (subgrain) within armored grain of Figure 8b, showing scattered <100-nm light-colored grains
In addition to providing information about grainsize, the SEM allows investigation of chemical composition and its variation within an area of interest. For example, partial replacement of carbonate by silica adjacent to the Heart Mountain Detachment is readily visible in electron backscatter (Figure 9c) and X ray elemental mapping (Figure 9d). This silicification is not evident in routine petrographic analysis. The timing of this replacement – during faulting or long afterward – is not known.
Figure 9c (left). SEM image of fault contact at Jim Smith Creek. Volcanic-derived gouge denoted by darker gray band along left side of image; lighter gray area is carbonate, with patches of darker gray silica. Figure 9d (right). X ray mapping of Silicon (Si), same area as Figure 9c. Intensity of green color is proportional to abundance of Si. Partial replacement of carbonate with silica, decreasing with distance from the fault, is clearly shown.
Chemical analysis of cataclasite from White Mountain fault samples documents the presence of minerals comprising magnesium and silica, without carbonate, in the relatively dark gray area in the image (Figure 10, yellow outline). These elements, combined with lack of elevated concentrations of other elements such as K, Al, Fe, or C, indicate the dominance of magnesium silicate. As the cataclasites were derived by brecciation of carbonate rocks, principally dolomite (Ca Mg carbonate) and to a lesser extent andesite (which also contains Fe, Al, and some K), the magnesium silicate (such as forsterite, talc, or serpentine) represents an alteration product formed from the original rock. At White Mountain, the upper-plate dolomite has been metamorphosed by intrusion of a plug of andesite, which is nearly the same age as the faulting (some have thought that the intrusion triggered the faulting by injecting gas or otherwise altering mechanical properties of the fault – shards of volcanic glass are locally present in the cataclasite). The origin of the observed magnesium silicate in the cataclasite is not known: it could have formed as a result of contact metamorphism of dolomite by the andesite magma in the presence of quartz, or it could have formed by thermal decomposition of dolomite followed by recombination of resultant MgO with aqueous silica during the faulting event. Texturally, the magnesium silicate domain appears to be intergrown with aggregates of other grains within the cataclasite (Figure 8a, Figure 10), implying that it formed during faulting.
Figure 10. SEM backscattered electron image of area in cataclasite, White Mountain (sample shown in Figure 8a, field of view rotated 90° clockwise). Dark gray area outlined by yellow likely contains low (relative to Ca)-atomic number elements. X ray elemental mapping (right) of Mg, Si, and Ca, illustrates composition of that area as being high in Mg and Si and low in Ca, typical of a magnesium silicate rather than of dolomite (CaMg carbonate) from which the cataclasite was originally formed.
Geochemistry of fault rocks.
Whole-rock geochemical analysis was carried out by Actlabs in Don Mills, Ontario utilizing their 60-element “Research 4B2” package, their most-rigorous analytical scheme and a generally-accepted standard of analytical excellence. Major elements (described herein) were determined by lithium borate fusion followed by ICP-MS. Of particular value to this study (at this juncture) are major-element results from a suite of White Mountain samples including cataclasites and undeformed dolomites with which they were to be compared for purposes of evaluating chemical alteration within the fault zone (Table 1). This in turn can elucidate processes involving fluids that may add or remove elements from the fault; in particular, major-element data can allow evaluation of the role, if any, of pressure solution or any form of dissolution in the evolution of the fault rocks.
Although andesite is reported within the White Mountain fault rocks, it is not commonly observed in petrographic thin section. The cataclasites appear to comprise primarily carbonate minerals that were presumably derived from precursor dolomites, which are represented by the average of samples 12WM4B and 12WM5 in Table 1. At the same time, the cataclasites from White Mountain contain significant concentrations (several times those in the dolomites) of Al2O3, K2O, and SiO2. These, as well as other related elements, are contributed by small quantities of andesite and volcanic glass that are mechanically mixed with the cataclasite.
Table 1. Major element composition of cataclasite, clastic dike, and dolomite samples, Heart Mountain Detachment
| Sample | Rock type | SiO2 | Al2O3 | Fe2O3 | MnO | MgO | CaO | Na2O | K2O | TiO2 | P2O5 | LOI | Total |
| 12WM1 | carb cata | 7.4 | 1.91 | 1.09 | 0.022 | 12.44 | 38.01 | 0.14 | 0.41 | 0.092 | 0.07 | 37.05 | 98.62 |
| 12WM2 | carb cata | 7.74 | 2.02 | 1.18 | 0.022 | 12.71 | 38.85 | 0.11 | 0.52 | 0.099 | 0.06 | 35.89 | 99.2 |
| 12WM3 | carb cata | 7.5 | 1.99 | 1.15 | 0.022 | 12.76 | 38.58 | 0.07 | 0.45 | 0.099 | 0.06 | 36.09 | 98.79 |
| 12WM4B | dolo | 2.09 | 0.34 | 0.34 | 0.01 | 7.97 | 44.79 | 0.05 | 0.07 | 0.016 | 0.02 | 43.04 | 98.73 |
| 12WM5 | dolo | 3.6 | 0.71 | 0.55 | 0.015 | 11.48 | 39.92 | 0.09 | 0.1 | 0.031 | 0.02 | 42.06 | 98.58 |
| 12WM8 | carb cata | 11.83 | 2.84 | 1.72 | 0.029 | 12.17 | 36.8 | 0.22 | 0.7 | 0.148 | 0.08 | 32.02 | 98.56 |
| 12WM10 | carb cata | 8.18 | 2.1 | 1.24 | 0.022 | 12.28 | 38.32 | 0.16 | 0.68 | 0.102 | 0.06 | 36.27 | 99.42 |
| 12WM16 | clastic dike | 11.61 | 2.39 | 1.43 | 0.023 | 10.17 | 42.24 | 0.03 | 0.46 | 0.108 | 0.05 | 30.49 | 99 |
| 13HM2-2 | carb cata | 1.39 | 0.32 | 0.26 | 0.011 | 20.54 | 30 | 0.05 | 0.16 | 0.016 | 0.03 | 45.92 | 98.71 |
| 13JS3 | clastic dike | 56.57 | 14.41 | 5.52 | 0.081 | 4.28 | 7.39 | 2.85 | 2.79 | 0.57 | 0.18 | 5.87 | 100.5 |
| 13JS4 | clastic dike | 40.05 | 7.4 | 3.27 | 0.265 | 3.17 | 22.9 | 1.32 | 0.95 | 0.303 | 0.1 | 18.94 | 98.67 |
“carb cata” = carbonate cataclasite; “dolo” = dolomite. “WM” samples are from White Mountain, “HM” from Heart Mountain, and “JS” from Jim Smith Creek. See Figure 1 for locations.
To account for the contribution of andesite to the major-element composition of the cataclasites, and thus remove it for the purposes of evaluating the effect of fluid-assisted mass addition or dissolution, the mass percentage of andesite was calculated for each sample based on the composition of known dolomite (Table 1) and an “average” andesite composition obtained from published sources (no White Mountain andesite was collected; this is a future endeavor). On the basis of these two end-member compositions, the weight % of andesite in each cataclasite sample was computed using a variety of elements (Table 2): SiO2, Al2O3, K2O, TiO2, Fe2O3, and CaO. The relative solubilities of these elements typically vary significantly in aqueous fluid: Al2O3 and TiO2 are generally insoluble, whereas SiO2, K2O, and CaO are highly mobile under a wide range of subsurface conditions. Fe2O3 is variable in its behavior. Notably, for a given sample, the calculated weight percent of andesite is nearly the same regardless of which element is used for the calculation, indicating that the sample composition is largely the product of mechanical mixing of dolomite and andesite and is little affected by the addition or removal of soluble elements, which would be expected to yield results substantially different from those based on insoluble elements in this sample suite if they had been mobile. For example, if calcium had been removed by dissolution (of calcite, for example) whereas aluminum had not, the amount of andesite calculated on the basis of Ca content of the cataclasite would be significantly greater than that calculated on the basis of Al. Specifically, if 25% of the mass of the cataclasite were removed in the form of CaCO3, the mass percentage of andesite calculated on the basis of CaO mass in the sample would be more than doubled, whereas it would increase by about 33% if it were calculated on the basis of an immobile element such as Al2O3. Overall, however, that is not the case, neither for Ca nor for K or Silica (Table 2); calculated andesite fractions are essentially the same regardless of the element used for that determination.
Table 2. Weight percent andesite calculated for White Mountain samples, as discussed in text. Abbreviations for rock type are the same as for Table 1.
| % andesite / (and+WM dolo) | Rock type | %And Al2O3 | %And K2O | %And TiO2 | %And Fe2O3 | %And SiO2 | %and CaO | Average | Std. Dev |
| 12WM1 | carb cata | 9.57 | 8.30 | 9.43 | 8.54 | 8.41 | 12.29 | 9.4 | 1.5 |
| 12WM2 | carb cata | 10.33 | 11.11 | 10.39 | 9.73 | 9.04 | 9.91 | 10.1 | 0.7 |
| 12WM3 | carb cata | 10.12 | 9.32 | 10.39 | 9.33 | 8.60 | 10.68 | 9.7 | 0.8 |
| 12WM4B | dolo | -1.28 | -0.38 | -1.03 | -1.39 | -1.39 | -6.89 | -2.1 | 2.4 |
| 12WM5 | dolo | 1.28 | 0.38 | 1.03 | 1.39 | 1.39 | 6.89 | 2.1 | 2.4 |
| 12WM8 | carb cata | 15.99 | 15.71 | 17.14 | 16.88 | 16.59 | 15.71 | 16.3 | 0.6 |
| 12WM10 | carb cata | 10.88 | 15.20 | 10.81 | 10.52 | 9.85 | 11.41 | 11.5 | 1.9 |
| 12WM16 | clastic dike | 12.88 | 9.58 | 11.63 | 13.04 | 16.19 | 0.33 | 12.6 | 2.4 |
Thus it is clear that there has been no significant mobility of major elements relative to one another in the cataclasites, hence no pressure solution.
Physical modeling of the Heart Mountain detachment
For purposes of evaluating the mechanical conditions necessary for movement, as well as estimating the actual speed of the block and duration of its movement, the huge slide above the Heart Mountain Detachment can be modeled simply as a block that slid down a gentle slope on a surface whose coefficient of friction may be quite low. The forces acting on the block are illustrated in Figure 11. For each square meter area of block,
Weight W= rgh,
where r is the density of the rock, g is acceleration due to gravity, and h is the thickness of the block (in meters in this case). [The website editor does not support symbol font, hence all Greek symbols are shown as English alphabet letters.] The block exerts a force Fn normal to the detachment equal to
Fn= rghcos(q),
where q is the slope of the detachment. This normal force is partly offset by fluid pressure in the detachment, which exerts an oppositely-directed force that reduces the normal force by the factor
l = Pfluid/rgh
The effective normal stress (written as an effective normal force, Fn eff) acting on the detachment, then, is
Fn eff = (1-l)rghcosq
In a similar vein, the block tends to slide down the slope under the force of its own weight parallel to that slope (Fpar). This force is not affected by the fluid pressure. This component of force is given as
Fpar = rghsinq
The force tending to push the block down the slope under its own weight is resisted by a frictional force Ff on the fault, which is characterized by a frictional coefficient m. The frictional resistance is written as
Ff = mFneff.
Substituting for Fneff,
Ff = m(1-l)rghcosq.
The net force acting on the block parallel to the detachment, then is
Fnet = Fpar – Ff, or
Fnet =rghsinq – m(1-l)rghcosq
Figure 11. Block model for Heart Mountain Detachment Fault calculations, discussed in text.
To calculate speed of the block, simple physics is employed.
Fnet = m a,
where Fnet is defined above, m is the mass of the block per m2 area (calculated as m = rh), and a is the acceleration of the block down the slope. Since the forces are calculated per square meter of fault area, this calculation is not dependent on the actual area of the block, only the variables used in the equations above. The block starts at zero velocity, then accelerates due to the action of Fnet being positive (the frictional resistance is not sufficient to arrest the block’s motion). Speed, the scalar of velocity, is calculated as
S = a t,
where t is time
Time must be constrained independently. The block could have moved for mere seconds, or for hours. However, the longer it moves, the model requires to move faster and farther. Here, a calculation of block speed is based on a total movement distance of 10 km: based on geologic reconstruction (Fig 2), this distance is appropriate for White Mountain. Blocks farther to the southeast have moved commensurately greater distances. In any event, the model can assume that the block accelerates uniformly to a maximum speed, reached at a distance of 5 km, then decelerates at the same rate to come to rest at a total distance of 10 km. Alternatively, the model can assume that acceleration continues for the entire 10 km, then the block stops instantly (or nearly so, realistically).
The motion distance (d) constrains the duration of motion through
d = s t
Speed s constantly increases due to acceleration over time t; the two parameters combine to produce the net displacement d. Thus in the model, the parameters discussed above are varied separately, and maximum speed (and duration of movement) are determined at a final block travel distance of 10 km.
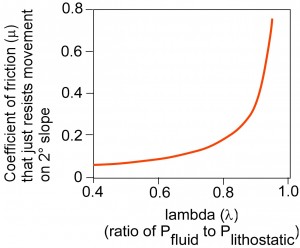
In the model, three parameters are varied independently of one another: l, m, and q. Each of these is considered in turn. 1) Elevated fluid pressure is commonly invoked as a way to “lubricate” faults, making movement easier. In this case, CO2 liberation due to thermal decomposition of calcite/dolomite is thought by Anders et al. (2010) to provide this elevated pressure. Hydrostatic fluid pressure in the fault, corresponding to a water table at the top of the block and interconnected porosity (either fractures or intergranular porosity) to the fault, results in l on the order of 0.45. Because the upper plate was likely fractured, and the stress regime during movement was such that the maximum compressive stress (s1) was essentially vertical, it is not likely that the fluid pressures approached lithostatic. Significantly overpressured fluids would almost certainly have quickly escaped from the fault, especially near the edges of the blocks; such reduction of fluid pressure would have tended to arrest motion. The common escape of fluids from the fault is recorded in the form of abundant clastic dikes in the upper plate. In some places, such as at Jim Smith Creek, the clastic dikes contain carbonate material whereas the fault gouge at that locality comprises andesite: the dikes must have formed earlier in the fault history when they lay above a portion of the fault that contained carbonate cataclasite. Uneven distribution of fluid overpressure in the fault, with some areas more-overpressured than others, would have created a patchwork of blocks moving at different speeds, likely fragmenting the blocks more than actually is the case. A maximum l of 0.7 was used for the modeling. 2) Coefficient of friction for typical rocks in the brittle regime is on the order of 0.7 – 0.9, although clays or other minerals can substantially lower m. However, experiments by Han et al. (2007) on thermal decomposition of calcite during frictional faulting suggests that the coefficient of friction in these materials could be as low as 0.06. There is controversy as to how low fault m can be; for this calculation, this m value takes into account any process involved in resisting motion on the fault and so may be a ‘catch-all’ for viscous flow mechanisms as well. The fault almost certainly had low coefficient of friction because of its extreme thinness in most places where observed: only by this mechanism would the fault have the necessary properties to allow movement across its entire extent and at all times. Fluid overpressure would be too variable, both spatially and temporally, to serve as a primary mechanism for facilitating movement. Low coefficient of friction, however, requires only a continuous surface, regardless of thickness, for it to facilitate movement. In this model, m is taken as low as 0.03; it turns out that low m is essential to movement on the detachment at any reasonable value of l; see Figure 12. 3) Slope q is constrained to be around 2° – 3°; if it is much more than 3°, the block moves so fast that it defies credulity. Thus this variable is closely constrained on the upper limit, although it could be as low as 1° or so on the lower limit.
Figure 12. Coefficient of fault friction (m) that just resists movement (m = tanq) on the fault versus that parameter l. For hydrostatic l, very low coefficients of friction, on the order of 0.06, are needed to allow movement on a 2° slope. Only at unrealistically high values of l (>0.9) would ‘normal’ fault m values be permissible in an active detachment.
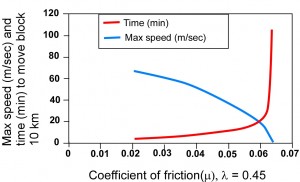
Given that m in the fault must be low, it can be varied to determine the maximum speed, in this case, after enough time to allow the block to move 10 km, accelerating the entire time (Figure 13). These calculations are for l of 0.45, equivalent to hydrostatic fluid pressure in the fault. The blue curve indicates that, for likely m values on the order of 0.05, the maximum speed at a block movement distance of 10 km is about 40 m/sec, or about 89 miles per hour. The duration of movement is part of this calculation, and is shown in Figure 13 by the red curve. For a m of 0.05, the White Mountain block would take about 15 minutes to move the 10 km distance. That’s really moving, considering the block is over a mile on a side by nearly a mile thick.
Figure 13. Speed and duration of movement of fault block subject to forces shown in Figure 11 versus fault coefficient of friction, with l of 0.45 (hydrostatic fluid pressure). Notably, m > 0.065 is sufficient to prevent or arrest movement.
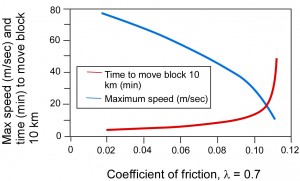
Similar calculations have been done for l of 0.7, or moderately overpressured fluids (Figure 14), just to account for the possibility that CO2 liberation or localized aquathermal pressuring of aqueous fluid in the fault may have boosted fluid pressure, even if only transiently. The solutions are of the same form as in Figure 13 but are shifted to slightly higher coefficients of friction, as would be expected in that elevated fluid pressure facilitates fault movement in the same way as decreasing m. Here, a coefficient of friction of 0.05 produces a maximum speed of about 60 m/sec, or 133 mph; a higher m of, say, 0.10 would be associated with a maximum speed of about 26 m/sec (58 mph). In nearly all cases, the maximum speed for the block that traveled 10 km is on the order of tens of miles per hour. This contrasts sharply with the results of physical modeling (based on questionable assumptions) of Craddock et al. (2009) that concluded that the same block likely reached maximum speed of 760 miles per hour. This supersonic speed is unsupported by any evidence or theoretical basis.
Figure 14. Calculation of maximum speed (blue curve) and duration of movement (red curve) for block in Fig. 11, given l of 0.7.
These values are maxima, as the model assumes acceleration throughout the 10-km travel distance, followed by an immediate stop. In the event that acceleration was followed by equal deceleration, the block would have reached a maximum speed at 5 km travel distance, then slowed to a stop by 10 km. Thus the maximum speeds, being linearly related to a constant net force, would be half those calculated here. Conversely, these speeds are likely less than is the case for blocks such as Heart Mountain and McCulloch Peaks, which traveled 30 to 45 km.
What made the block stop? If the detachment slope decreased in the direction of movement, for instance ramping uphill, one would expect the block to slow and perhaps stop. How the carbonate slab rode up and over the ramp at Dead Indian Pass, which now has about 1 km of structural relief on the Heart Mtn Detachment but which was also likely an upslope portion of the detachment 50 million years ago, is anyone’s guess. But climb it must have, because Heart Mountain comprises a nearly flat-lying block of crinoidal Paleozoic carbonate that must have originated north of Dead Indian. Many of the blocks that still lie atop very gently southeast-dipping Paleozoic carbonates north of Dead Indian (Fig. 2) do not appear to have encountered changes in detachment slope and likely stopped for other reasons. Changing material properties (e.g., coefficient of friction and all that encompasses) and/or fluid pressures could also be responsible for changes in block speed. For the block to continue moving, there must have been a balance between frictional resistance to movement, which generated heat, and the lowering of coefficient of friction and/or raising of fluid pressure, which facilitated movement, reducing the generation of heat. This delicate balancing of movement and resistance to movement operated over large areas and long distances of movement. Lowering of fault coefficient of friction complemented and likely dominated the ‘lubrication’ provided by the generation of CO2 by thermal decarbonation. Cooling of the fault (by means of decreasing the slope or changing material or fault mechanical properties) through a critical temperature that caused decarbonation to slow could have produced a feedback that ultimately caused the block to stop.
Discussion
The foregoing study demonstrates that the narrow cataclasite zone likely had unusually low coefficient of friction, and that blocks sliding downhill on the detachment accelerated from a standstill to speeds of up to about 100 miles per hour before the block stopped moving. The low coefficient of friction is possibly due to the extremely fine grainsize produced by thermal decomposition of carbonate that itself resulted from frictional heating on the fault. This sequence of events appears somewhat circular: movement was needed to generate CO2 which was needed to aid movement. But in all likelihood, the initial movement was not CO2-aided but rather simply the result of a volcanic tremor that caused the rocks to break at one or more points along their bedding. Once the sliding started, however, frictional heating could have produced the necessary temperatures within seconds; the rupture then propagated outward from these failure zones and linked together, and then the whole block let loose. The thermal decarbonation mechanism obviously requires the presence of carbonate rock, but it appears to have been necessary on only one side of the fault: Heart Mountain and McCulloch Peaks lie atop shale and sandstone with no carbonate beneath them, and the operation of thermal decarbonation in terms of producing the necessary low frictional coefficient must have been restricted to cataclasites derived from the upper plate.
The movement of the detached rocks must have been an astonishing event: an entire block the size of Rhode Island, so big that it could not be glimpsed in its entirety, rumbling and roaring and who knows what else as it slid and fragmented downslope, breaking up and out onto the land surface, huge rafts gouging the ground as they slid. Imagine being able to witness such a spectacle from a safe vantage point! This sort of event should give pause to disaster mitigation workers in cities that lie at the base of mountains that contain thick carbonate rocks, such as Salt Lake City. Although the circumstances that aligned to produce the Heart Mountain slide were highly unusual, smaller but nonetheless disastrous events are possible worldwide.
References cited
Anders, M. Fouke, B., Zerkle, A, Tavarnelli, E., Alvarez, W., Harlow, G., 2010, The role of calcining and basal fluidization in the long runout of carbonate slides: An example from the Heart Mountain Slide Block, Wyoming and Montana, U.S.A.; Jour. Geology, v. 118, pp. 577-599
Beutner, E. C., and Gerbi, G. P. 2005. Catastrophic emplacement of the Heart Mountain block slide, Wyoming and Montana, U.S.A. Geol. Soc. Am. Bull. 117: 724–735.
Beutner, E., Hauge, T., 2009, Heart Mountain and South Fork fault systems: Architecture and
evolution of the collapse of an Eocene volcanic system, northwest Wyoming; Rocky Mtn. Geology, v. 44, pp. 147-164
Boullier, A-M., Yeh, E-C., Boutareaud, D., Song, S-R., Tsai, C-H., 2009, Microscale anatomy of the 1999 Chi-Chi earthquake fault; Geology, Geophysics, Geosystems, v. 10., no. 3, doi 10.1029/2008GC002252
Craddock, John P; Malone, David H; Magloughlin, Jerry; Cook, Avery L; Rieser, Michael E; et al., 2009, Dynamics of the emplacement of the Heart Mountain Allochthon at White Mountain; constraints from calcite twinning strains, anisotropy of magnetic susceptibility, and thermodynamic calculations; Geological Society of America Bull.121: 919-938
Craddock, J., Geary, J., Malone, D., 2012, Vertical injectites of detachment carbonate ultracataclasite at White Mountain, Heart Mountain detachment, Wyoming; Geology, vol. 40, pp. 463-466
Douglas, T. A.; Chamberlain, C. P.; Poage, M. A.; Abruzzese, M.; Shultz, S.; Henneberry, J.; and Layer, P. 2003.Fluid flow and the Heart Mountain fault: a stable isotopic,fluid inclusion, and geochronologic study. Geofluids 3:13–32.
Han, R., Shimamoto, T., Hirose, T., Ree, J.H., Ando, J.i., 2007. Ultralow friction of carbonate faults caused bythermal decomposition. Science 316. http://dx.doi.org/10.1126/science.1139763.
Hauge, T, 1993, The Heart Mountain detachment, northwestern Wyoming: 100 years of controversy, in Snoke, A.W., Steidtmann, J.r., and Roberts, S.M., eds., Geology of Wyoming: Geol Surv. Wyo. Memoir 5, p. 530-571
Malone, D., Hauge, T; Beutner, E., 1999, Field guide for the Heart Mountain detachment and associated structures, Northeast Absaroka Range, Wyoming; Geol. Soc. Amer. Field Guide1, pp. 177-201
Mitchell, T., Smith, S., Anders, M., DiToro, G., Nielsen, S., et al.., 2015, Catastrophic emplacement of giant landslides aided by thermal decomposition; Heart Mountain, Wyoming; Earth and Planet. Sci. Lett. v. 411 pp. 199-207.
Pierce, W., 1973, Principal features of the Heart Mountain fault and the mechanism problem, in DeJong, K., Scholten, R., eds., Gravity and Tectonics: New York, John Wiley and Sons, pp. 457-471
Rempe, M.;Smith, S.; Ferri, F.; Mitchell, T.; Di Toro, G., 2014, Clast-cortex aggregates in experimental and natural calcite-bearing fault zones; Jour Struct. Geol., v. 68, pp. 142-157.
Rowe, C., Fagereng, A., Miller, J., Mapani, B., 2012, Signature of coseismic decarbonateion in dolomitic fault rocks of the Naukluft Thrust, Namibia; Earth Planet. Sci. Letters, v. 333, pp. 200-210
Swanson, E., 2015, Structural and clumped-isotope constraints on the mechanisms of displacement along low-angle detachments; unpub PhD thesis, Calif Instit. Tech., 193 pp.
Templeton, A. S.; Sweeney, J. J.; Manske, H.; Tilghman, J. F.; Calhoun, S. C.; Violich, A.; and Chamberlain, C. P. 1995. Fluids and the Heart Mountain fault revisited. Geology 23:929–932