Theory

of

Sustained Optimal Challenge

in

Teaching and Learning

Yerkes-Dodson law suggests an optimal level of arousal for the best performance in learning tasks. Ideally, the instructors’ expectations should match the abilities and inabilities of students. This study proposes a theory that challenges students optimally and continually over the course of teaching and learning, with proofs using both theoretical and classroom examples. The theory of sustained optimal challenge facilitates student learning by achieving primarily three objectives: (1) continually adjusts the speed and content difficulty levels over the course of teaching and learning; (2) matches the instructors’ expectations with the students’ aptitudes (abilities and inabilities); and (3) finally, reduces the variation in student learning. The effect of central limit theorem, teaching and learning theories, learning outcomes, and student feedback supported the proposed theory in a wide range of disciplines, including, Statistics, Mechanics, Quality, and Ergonomics. Sustained optimal challenges were observed in most courses taught utilizing the proposed theory.

Why Do We Need Another Theory?

Bloom suggests that students should be taught in a way so that they could become a master by learning 90% of the materials (Bloom, 1968). In practice, students move up to the next level even with 60% learning from a topic. In some education systems, students can proceed to the next level just by learning only about 33% of the materials (one of the author’s earlier institutions). Therefore, the exposure to the advanced level topics has been prioritized more than the mastery learning in many education systems (Wayne, Barsuk, O’Leary, Fudala, & McGaghie, 2008). However, how much material at what difficulty levels should a student learn to become a master in that area, or to proceed to the advanced level topics? The definition of mastery or the level and amount of content the students are exposed to could be relative to the instructors and the level of students’ abilities and inabilities. The following is an excerpt from the learning outcomes of a course.

“Student should be able to apply anthropometry to design, redesign, develop, and evaluate workstations.” A simple chair design to a complex workstation for a physically and mentally impaired individual could be used as an example to accomplish the same learning outcome mentioned above. Is the students’ learning outcome the same from using a very simple to a very complex problem-solving practice? How difficult is too difficult for the students? How do we know that we are challenging students optimally? How do we ensure that the students are getting the opportunity to apply their full potential, and move up to the next advanced level? The classic Yerkes-Dodson law suggests the theory of optimal level of arousal for the best performance (Figure 1) (Yerkes & Dodson, 1908).

To achieve the optimal level of arousal, the expectation from an instructor should neither be too high nor too low. Each student should be taught using the method particularly suited for that student, and he/she must be provided with enough time to master the materials (Bloom, 1968; Carroll, 1963; Tomlinson, 2014). Ideally, the instructors’ expectations should match the students’ learning abilities and inabilities (Figure 2).

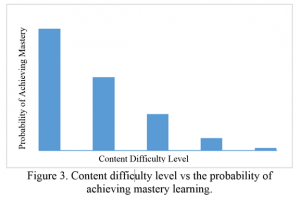
Figure 3 represents a relationship between the difficulty level and the mastery on a subject matter. If the material difficulty level is too low, many students will achieve the highest level of mastery (Meier, 2004; Ziomek & Svec, 1997). However, the students’ full potential for growth may not be achieved through easy challenges (Clifford, 1990). Often, low expectation levels result in an unpreparedness for the higher education or entering the workforce (Meier, 2004; Zimmerman & Dibenedetto, 2008). In contrast, if the content is too difficult, few students will achieve the highest level of mastery within the allocated time (Carroll, 1963). Therefore, the extent to which a student is taught affects their arousal level resulting in the change in learning performances. One way to avoid too many easy or difficult topics is to use a normal distribution (Bloom, 1968). The normal distribution difficulty level is also justified by the fact that the students’ aptitudes (abilities and inabilities) are observed to be normally distributed (Bloom, 1968; Fletcher, Denton, & Francis, 2005). In a normally distributed difficulty level, only a few students will find the challenges too difficult or too easy, which may result in an optimum level of difficulty for the majority of the students.

Many studies have suggested that students should be challenged optimally to provide the best learning opportunities (Fink, 2013; Wiggins & McTighe, 2005). Furthermore, the optimal challenge has to continue over the course of learning to enhance the self-regulated learning (Nicol & Macfarlane‐Dick, 2006). However, a clear and practical pathway to achieve the sustained optimal challenge has yet to be developed in classroom instructions. The objective of this study is to suggest a theory to challenge students optimally over the course of teaching and learning.

How To Implement It?

The sustained optimal challenge was achieved utilizing multiple assessments with regular feedback on the students’ performances over the course of learning. The difficulty levels for the materials were adjusted continually to enhance learning (Gee, 2005). To enhance student learning, multiple assessments ensured the sustained optimal challenge, primarily in three ways.

First, the multiple assessments provide an opportunity for the instructor to continually improve the course through real-time communication with the students resulting in better students’ performances (Beatty, 2005; Shumin, 2002). Second, the multiple assessments ensure the difficulty level is normally distributed according to the “central limit theorem.” The central limit theorem states as following (Adams, 2009).

Figure 4 provides an example proof for the central limit theorem. A six face fair die random variable is uniformly distributed with equal probability of 1/6 for each side. Figure 4 shows the distribution of the averages of 1, 2, 3, 4, 5, and 8-dice random variables.

Figure 4 indicates that the linear distribution of a single die converges into a normal distribution when the mean (or sum if the sample size is same) values of the sample points from draws of multiple dice at a time is used. The similar phenomenon can be observed for any other type of original distribution of a set of random variables (Adams, 2009).The distribution becomes more Gaussian using more dice at a time. Moreover, the variability decreases as the number of dice increases (Figure 4) (Cochran, 2007). Therefore, the third and final advantage of multiple assessments is to reduce variability in student learning, which is highly recommended by the education scholars (Bloom, 1968; Guskey, 2007; Ladson-Billings, 2006; Nicol & Macfarlane‐Dick, 2006; Orfield, Losen, Wald, & Swanson, 2004; Tomlinson, 2014).

Approximately 10-13 assessment points (one assessment per week) for a three-credit hour course in a semester system teaching were set to adjust the speed and difficulty levels of the course to challenge the students optimally. Based on a pretest performance, the material for the first assessment was assigned. A poor performance in the earlier test indicated too high difficulty level for the students and vice versa. Therefore, the performance of the first assessment was utilized to change the speed and difficulty level of the materials for the second assessment, and so on. The process of continual adjustments for the material difficulty levels proceeded using 10-13 assessments during the course of teaching and learning to keep the challenge optimal for the majority of the students. Furthermore, in addition to the end of the semester student feedback, at least one mid-semester student feedback was also collected for all the courses taught using the theory.

What Results Do We Expect?

Utilizing the sustained optimal challenge theory, a wide range of multidisciplinary courses was taught in undergraduate and graduate levels. The author shares the class size, student evaluation, and grade distribution from five courses, including, (1) Introductory Statistics, (2) Mechanics of Materials, (3) Quality Management Systems, (4) Human Factors and Ergonomics, & (5) Design of Experiments. These courses include the combination of undergraduate, undergraduate/graduate, and graduate levels. The grades earned by the students were observed to be approximately normal distributions with a “B” average for undergraduate courses and an “A” average for the graduate courses.

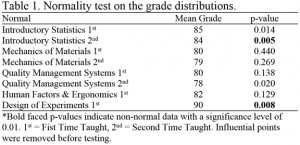
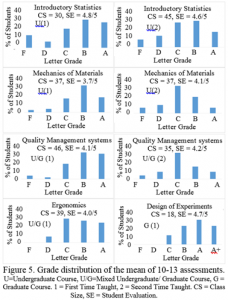Table 1 shows normality analysis using the Chi-square goodness of fit test. The distribution of the mean grades followed a normal distribution with a level of significance of 0.01, for six out of eight courses taught using the theory of the sustained optimal challenge. The mean grades earned were observed to be different between courses as well as the level of the courses (undergraduate or graduate).

The mean student evaluations were observed to be 4.25 (weighted by the number of students) on a scale of 5, relatively satisfactory to the expectations of the instructor and the institution. The ten most frequent positive feedback from the courses taught using the sustained optimal challenge theory, includes: (1) instructor is knowledgeable; (2) instructor really cares for us; (3) focus on student learning; (4) problem solving step by step; (4) learned a lot from this course; (5) very effective use of class time; (6) approachable and easy to talk; (7) good response to students’ questions; (8), fair grading; (9) clear expectation; and (10) small deadlines.

What Do Educators Think About It?

The Theory of the Sustained Optimal Challenge has helped student learning primarily in three ways discussed below.

Frequent Assessments and Feedback in a Consistent and Timely Manner for Continual Improvement

The frequent assessments and feedback on students’ performance helped both the students and the instructor resulting in a significant gain in learning (Black & Wiliam, 1998; Fink, 2013). As the students learn their mistakes continually over the course of learning, the instructor also sees the opportunity in teaching so that students do not make the same mistakes in the future. Frequent assessments and feedback facilitate learning by introducing: (1) self-regulated learning (Nicol & Macfarlane‐Dick, 2006); (2) mastery learning (Zimmerman & Dibenedetto, 2008); (3) improved communications between students and the instructor (Beatty, 2005); (4) learning motivation (Keller, 1987); (5) habit to regular study (Britzman, 2012); (6) more retention of the materials taught earlier (Karpicke & Roediger, 2008) creates an interest for gaining new knowledge (Tobias, 1994); and (7) instructor’s knowledge on students’ progresses, abilities, and inabilities resulting in an optimal adjustment over the course of learning (Angelo & Cross, 1993). Particularly the frequent assessments and feedback help the instructor to adjust the course continually, instead of waiting for the end of the semester feedback from the students, which rarely have any direct effect on the current students.

Figure 6 describes a typical course development life cycle (CDLC) (Blanchard & Fabrycky, 2014; Fink, 2013; Wiggins & McTighe, 2005). The CDLC could be applied in each assessment period (Figure 7), rather than waiting for the student feedback/assessment at the end of the semester. Therefore, the frequent assessments facilitate the continual improvement over the course of learning similar to Kaizen quality improvement philosophy (Figure 7) (Masaaki, 1986). Kaizen quality philosophy suggests that quality should be improved every day, everywhere, and by everybody (Masaaki, 1986).

Matching the Instructors’ Expectations with the Students’ Aptitudes (abilities and inabilities)

The final grade distributions for most courses have been observed to be approximately normal using this method of instruction because of the effect of central limit theorem. As the students’ aptitudes (abilities and inabilities) have been observed to be normally distributed (Bloom, 1968), a normally distributed difficulty level would facilitate the optimal challenge for the majority of the students. However, the learning outcome distributions have not been observed as normal as predicted by the central limit theorem (only 6 out of 8 courses have been observed to be normal) (Table 1). If the performance on the prior materials affects the performance of the next assessments, the assumption of independent random variables is refutable for students’ assessments (e.g. exam). Therefore, the mean grade could still follow an approximate normal distribution, but asymptotically for the non-normal grade distributions observed in the study (Rosenblatt, 1956).

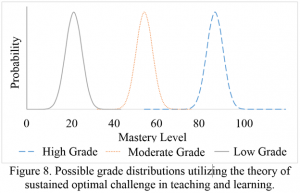Although grade should not be assigned by a random chance (as if curving in a normal distribution), many education systems prefer normally distributed grading (Bloom, 1968). In some education systems, only 33% is used as the passing grades and 80% or more as the best grade (one of the author’s earlier institutions), whereas some education systems use 60% as the passing grade. In the author’s current institution, 70%-80% (letter grade C) is used as the passing grade for graduate and many undergraduate programs. Figure 8 shows a few possible grade distributions using the sustained optimal challenge theory. It is possible that most students in the class would earn the highest grade (e.g. letter grade A) with a normally distributed percentage of learning due to the effect of central limit theorem (the right most distribution in Figure 8). Figure 8 shows that sustained optimal challenge can be achieved in any grading situations, including the education systems ranging from 33% passing grades to the 70% passing grades. This research demonstrates a way to sustain an optimal challenge for students over the course of teaching and learning, without suggesting any mean grade. The grades should reflect their learning, rather than a random chance.

Significant Reduction in Variation in Student Learning

One of the major advantages of the theory of sustained optimal challenge is the inherent reduction in the variation in learning according to the central limit theorem (Figure 4). Figure 4 demonstrates that as the number of observations (assessments) increases, the overall variances significantly decreases (the distribution converges from a flatter to a narrower normal distribution) (Figure 4) (Owen, 1992). Education scholars unanimously suggest reducing variation in student learning (Bloom, 1968; Guskey, 2007; Lieberman & Hoody, 1998). The theory of sustained optimal challenge inherently reduces the variation in student learning (Figure 9). Research on frequent assessments observes the reduction in variation in student learning (Karpicke & Roediger, 2008).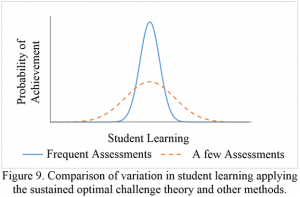

Limitations and Future Studies

According to the central limit theorem, the average or sum of multiple trials from a set of independent and identical random variables are normally distributed. Unlike a fair die, the instructors’ assessments could produce a biased result. For example, sometimes a take-home test could produce a biased result which violates the assumptions of the independent and identical random variables for the central limit theorem. These biases must be kept at a minimum to create a normally distributed difficulty level. The learning outcomes have not been compared to the courses taught using the theory of sustained optimal challenge and other methods of instruction.

The Final Thoughts

This research presented a theory to challenge students optimally over the course of teaching and learning. The theory suggests that frequent assessments and regular feedback help students’ learning primarily in three ways: (1) continual improving over the course of teaching and learning; (2) matching the instructors’ expectations with the students’ aptitudes (abilities and inabilities); and finally (3) reducing the variation in student learning. The instructor will be able to set the depth of the contents and the speed of instructions to prepare students to cope with the future challenges in the higher education or the workforce.

References

Adams, W. J. (2009). The life and times of the central limit theorem. Providence, R.I.; [London]: American Mathematical Society ; London Mathematical Society.

Angelo, T. A., & Cross, K. P. (1993). Classroom assessment techniques: A handbookfor college teachers. San Francisco: Jossey-Bass.

Beatty, I. D. (2005). Transforming student learning with classroom communication systems. arXiv preprint physics/0508129.

Black, P., & Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education: principles, policy & practice, 5(1), 7-74.

Blanchard, B. S., & Fabrycky, W. J. (2014). Systems engineering and analysis. Essex: Pearson.

Bloom, B. S. (1968). Learning for Mastery. Instruction and Curriculum. Regional Education Laboratory for the Carolinas and Virginia, Topical Papers and Reprints, Number 1. Evaluation comment, 1(2), n2.

Britzman, D. P. (2012). Practice makes practice: A critical study of learning to teach: Suny Press.

Carroll, J. B. (1963). A model of school learning. Teachers college record.

Clifford, M. M. (1990). Students need challenge, not easy success. Educational Leadership, 48(1), 22-26.

Cochran, W. G. (2007). Sampling techniques: John Wiley & Sons.

Fink, L. D. (2013). Creating significant learning experiences : an integrated approach to designing college courses. San Francisco, CA: Jossey-Bass.

Fletcher, J. M., Denton, C., & Francis, D. J. (2005). Validity of Alternative Approaches for the Identification of Learning Disabilities Operationalizing Unexpected Underachievement. Journal of Learning Disabilities, 38(6), 545-552.

Gee, J. P. (2005). Learning by design: Good video games as learning machines. E-Learning and Digital Media, 2(1), 5-16.

Guskey, T. R. (2007). Closing achievement gaps: revisiting Benjamin S. Bloom’s “Learning for Mastery”. Journal of Advanced Academics, 19(1), 8-31.

Karpicke, J. D., & Roediger, H. L. (2008). The critical importance of retrieval for learning. science, 319(5865), 966-968.

Keller, J. M. (1987). Strategies for stimulating the motivation to learn. Performance Improvement, 26(8), 1-7.

Ladson-Billings, G. (2006). From the achievement gap to the education debt: Understanding achievement in US schools. Educational researcher, 35(7), 3-12.

Lieberman, G. A., & Hoody, L. L. (1998). Closing the Achievement Gap: Using the Environment as an Integrating Context for Learning. Executive Summary.

Masaaki, I. (1986). Kaizen: The key to Japan’s competitive success. New York, ltd: McGraw-Hill.

Meier, D. (2004). Many children left behind: How the No Child Left Behind Act is damaging our children and our schools: Beacon Press.

Nicol, D. J., & Macfarlane‐Dick, D. (2006). Formative assessment and self‐regulated learning: A model and seven principles of good feedback practice. Studies in higher education, 31(2), 199-218.

Orfield, G., Losen, D., Wald, J., & Swanson, C. B. (2004). Losing our future: How minority youth are being left behind by the graduation rate crisis.

Owen, A. B. (1992). A central limit theorem for Latin hypercube sampling. Journal of the Royal Statistical Society. Series B (Methodological), 541-551.

Rosenblatt, M. (1956). A central limit theorem and a strong mixing condition. Proceedings of the National Academy of Sciences, 42(1), 43-47.

Shumin, K. (2002). Factors to consider: Developing adult EFL students’ speaking abilities. Methodology in language teaching: An anthology of current practice, 12, 204-211.

Tobias, S. (1994). Interest, prior knowledge, and learning. Review of Educational Research, 64(1), 37-54.

Tomlinson, C. A. (2014). The differentiated classroom: Responding to the needs of all learners: Ascd.

Wayne, D. B., Barsuk, J. H., O’Leary, K. J., Fudala, M. J., & McGaghie, W. C. (2008). Mastery learning of thoracentesis skills by internal medicine residents using simulation technology and deliberate practice. Journal of Hospital Medicine, 3(1), 48-54.

Wiggins, G. P., & McTighe, J. (2005). Understanding by design: Assn. for Supervision & Curriculum Development.

Yerkes, R. M., & Dodson, J. D. (1908). The relation of strength of stimulus to rapidity of habit‐formation. Journal of comparative neurology and psychology, 18(5), 459-482.

Zimmerman, B. J., & Dibenedetto, M. K. (2008). Mastery learning and assessment: Implications for students and teachers in an era of high‐stakes testing. Psychology in the Schools, 45(3), 206-216.

Ziomek, R. L., & Svec, J. C. (1997). High school grades and achievement: Evidence of grade inflation. NASSP Bulletin, 81(587), 105-113.

Ahmed, S., (2017). Theory of Sustained Optimal Challenge in Teaching and Learning. Proceedings of the 2017 International Annual meeting of Human Factors and Ergonomics Society, Austin, TX, USA, October 9-13.

Presentation on the Theory of Sustained Optimal Challenge in Teaching and Learning